I’m back from the garage with some experimental results on cable routing friction, and they are really cool!
Above: Photo of my custom “Derailleur Cable Friction Tester”, loaded with a 12″ length of housing making a 180 degree turn at a radius of ~2″.
Recall from my previous post, I was wondering how best to accommodate the curve in routing the rear derailleur cable from the chainstay to the derailleur. A short tight hook, or a longer lazy curve? Historically I have preferred a long looping setup to a short tight hook. It turns out I may have been wrong.
With my custom derailleur cable friction tester, I was able to measure the cable force required to overcome the derailleur spring force in a variety of configurations – total direction changes from zero to 540 degrees and turns with radii down to 1.5″ and up to 5″.
It seems this Eytelwein guy’s capstan equation is right. The radius doesn’t matter. The length doesn’t matter. The only relevant parameters are total change in direction and coefficient of friction.
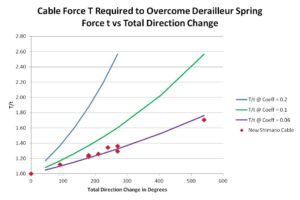The solid lines are theoretical T/t vs total change in direction for various coefficients of friction. The red dots are my experimental results for 12″ and 24″ length housings in various configurations. To the accuracy of my measurements, which is admittedly not laboratory grade, all my data points lie on a curve corresponding to the capstan equation with a friction coefficient of 0.06.
Above: A couple of the configurations I tested. Left: 24″ housing, 180 degrees, 5″ radius. Right: 12″ housing, 270 degrees, 2″ radius.
For a final test, I arranged my rig to place the cable in a configuration very much like it would be on a bike, from chainstay to derailleur.
Notice how the cable housing tends to curve out before beginning the main turn-around. This results in a total direction change of greater than 180 degrees. (Call it 15 degrees out, 15 degrees back to vertical, then 180 degrees – total direction change of 210 degrees.) And sure enough, the T/t ratio falls on the curve at ~210 degrees.
Constraining the cable so that it does not go through these extra direction changes should lower the required cable force, and it does!
Above: 12″ cable constrained to a simple 180 degree turn at a radius of ~1.5″.
The capstan equation predicts about a 3% drop in T/t and that is almost exactly what I observed.
I repeated my test with an old cable and housing in my rig and the results were almost identical. I was surprised that the friction coefficient was no higher than a new cable and housing (0.06). But what really surprised me was that adding a drop of light oil at each end of the housing increased the required force! Solving the capstan equation for friction coefficient I got a 0.08 for both the constrained and unconstrained configurations with oil.
OK, that’s been a journey. So how can we use this information? Here are my recommendations:
- Route cables to minimize total change in direction.
- Try to pre-form a tight but smooth curve in the cable housing near the derailleur to minimize the bowing effect that results in greater total direction change. My friend Brian suggested that a heat gun might be useful. If I see you riding with a zip-tie on your cable to hold it in to 180 degrees, I’ll laugh at you. Use clear packing tape. 🙂
- Don’t arbitrarily oil derailleur and brake cables. It may actually increase friction.
- Apply this information to derailleur and brake cables all over the bike.
- Appreciate SRAM’s recent mountain bike derailleur designs where the cable enters the derailleur more vertically than to the rear.
- Try not to lose sleep over this, because modern bicycle cable systems work very well. These tweaks will make only a very marginal, probably not discernable, difference.
One day I might do comparative testing on different manufacturers’ cables, or on various oils and greases. I may include some static friction testing. I may do brake cables. But for now I want to move on to other Esoteric Observations on Bicycles and Cycling.
A few closing disclaimers and comments:
- This is all dynamic friction. What I have reported is maximum required force to stroke the derailleur by hand at a dead-slow rate.
- As you might expect, the required force for any given configuration is not constant – or even linear – throughout the derailleur stroke. It starts out low, increases through a maximum at about mid-stroke, then declines.
- My new cables were Shimano stainless steel cable and Shimano OT-SP41 housing. I don’t know the brand of the old cables. They came off of Trekker’s Tarmac the other night.
- And if you just have to know – it takes about 5.8 KG (12-3/4 lbs) cable tension to stroke an old Ultegra 6700 derailleur.
Killa, that was an interesting experiment re: cable routing.
I have one for you, which I haven’t found a satisfactorily scientifically derived answer to.
Are disc brakes really any better than linear-pull rim brakes?
Disc brakes can be significantly more powerful than rim brakes, given that you don’t have to worry about either crushing the rim or stressing whatever the brakes are attached to (the fork or the frame’s rear triangle).
But… it seems to me that the very small circumference of a disc-brake disc, versus the widest-possible circumference of the rim would negate much, or even all the advantage of the increased power that discs give.
After all, it’s not raw power that we want in brakes – it’s the modulation that all that power affords. And it’s much easier to slow or stop a spinning wheel at its widest diameter/circumference than near its center.
Looking forward to your next experiment!
Hi Fred! Thanks for the comment. You’ve got me interested. Your first question “Are disc brakes really any better than linear-pull rim brakes?” Is impossible to answer without a technical definition of “better”. I googled “disc vs rim” and got like a gazillion hits. One more forum on all the pro’s and con’s won’t add anything new, so I won’t go there.
What intrigued me is the question you raise about the radius difference. There is no doubt that disc brakes can generate more stopping force at the tire/road (or trail) interface, for better or worse. The question is, how can a disc with a ~180mm diameter generate more stopping force than a rim brake with a diameter of 622mm – using the same hand force and range of motion – without breaking the laws of physics? I’ve got some ideas, but I want to take some measurements and do some calculations before I answer. I’ll post something in the next day or two.
Glad to see I’ve piqued your interest! I think what defines “better” in braking boils down to increased modulation. You’ll notice that sports cars not only have bigger, stronger calipers and pistons, but they also have larger diameter discs. Why? Even smaller disc brakes will lock (let’s leave ABS out of the picture for now). Similarly, any linear-pull brake on the front wheel has of any bike I’ve ever ridden has enough stopping force to lock the wheel at speed, and make the bike skid in a turn (on a loose or slippery surface) or make the bike flip over. And any caliper-type of brake (not just linear pull) that I’ve ever ridden can lock and make the rear wheel skid. So the raw stopping force is not what’s at issue. It’s how well you can modulate that stopping force — as in increments. Let’s say 0 is not braking, and 10 is a locked brake. A poorly modulated brake might go directly from 9 (braking very hard but still safely braking) to 10 (locked). But a better modulated brake might let you get to 9.5, or even 9.9, before going to 10. And something that makes modulation even more important is that what constitutes a “10” changes with the weather, the road surface and the condition of the tire. So you have to have better modulation throughout the entire range. To go back to the ABS issue in cars, nothing really changes here — the point is to modulate more precisely up to the point where the ABS has to kick in.
I think it’s about leverage, or mechanical advantage.
Brake lever has a fixed travel length, for obvious reasons:
– one limiting factor is an average hand length, so the lever can’t be very far from the bars.
– the other is the very existence of bars, a lever can only travel until it hits the bars (preferably, operating range should be even smaller, so that the lever can be operated with one or two fingers, not squeezing the other fingers still left on the bars).
So this leaves playing with the pad travel length. Disk brakes enable placing the pads much closer, so instead of traveling a few mm, they travel up to one mm, usually sitting even closer than that to the disk. Hydraulic system has other advantages on top of that, like elimination of cable friction, but the main benefit of disk vs rim brakes is the higher mechanical advantage due to significantly shorter pad travel distance.
Rim brakes need to be placed a bit further away from the rim, since the wheel will move more on the outer part – wheel flexing a bit under loads, not being 100% true etc.
There are a number of variables to consider, mechanical advantage at the lever, mechanical advantage at the caliper, brake surface area, coefficient of friction of the pad, material of the braking surface or coefficient of friction of the braking surface and travel. That is just the braking system. I would not be surprised to find that the diameter of the disk is related to temperature while braking.
Then there is the issue of forces generated and applied to the fork and frame all the way down to the hub. Your definitely don’t want radial spoke pattern for a disk brake!
Patrick,
Thanks for the comment. The torque load that a disc (or any other hub-mounted) brake system applies to the spokes is especially interesting to me.
It would be fun to lace up a disc wheel radially and see how much windup occurs.. and how long it takes the spokes to rip thru the eyelets.