Cable Routing and Friction

You know that loop of cable that runs from the rear chainstay to the rear derailleur? Did you ever wonder whether it’s better to make a long lazy loop, or to minimize the length with a tighter curve? Yep, me too.

My scientist friend Pierre told me the length of this loop doesn’t matter. This is based on something called the capstan equation. I have no recollection at all of such a thing from my college days. I must have been absent that day. I am familiar with the idea of a capstan, usually in the context of using a small force and friction to oppose a large force.

Imagine a truck with a rope tied to the trailer hitch. You can’t hold back the truck by holding onto the rope. The truck will drag you away. Now make a wrap around a tree – no knots, just walk once around the tree with the rope – and pull on the end. You can probably hold back the truck. If not, make another wrap. Very soon you will be able to hold back the truck with a light pull on your end of the rope (or Mr. Truck will pull the tree out of the ground.) This is the capstan effect in action. In this usage, the capstan effect works in your favor.

The capstan effect works against you in bicycle cabling. On a bicycle, you are Mr. Truck, and the derailleur spring is the person at the other end of the rope, resisting your efforts to shift (or brake). The capstan equation states that the force you must apply to overcome the derailleur spring force is proportional to the total change in direction and the coefficient of friction. In fact, it is exponentially proportional to the total change in direction and the coefficient of friction.

The radius doesn’t matter. The total length doesn’t matter. Only total change in direction and coefficient of friction.

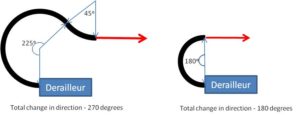Which arrangement would you think requires more cable force, the long gentle loop on the left, or the shorter tighter loop on the right. Apparently the long gentle loop, according to the capstan equation.

Truth in blogging disclaimer: This simple form of the capstan equation assumes a radius of curvature large enough that the cable can be considered flexible. For a derailleur or brake wire, it’s probably good down to about a 2-3″ radius. A curve tighter than that would require a more complex analysis. Google “capstan equation for strings with rigidity” if you are interested.

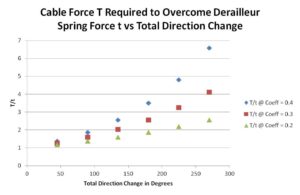The chart above shows the exponential increase in cable force required versus the total direction change of the cable for various friction coefficients.

This has big implications for how I will route derailleur and brake cables! I can tell you are as excited about it as I am. I’m off to the garage to do some experiments. I’ll be back in a few days with my results.